On the Processing Speed of the Human Brain

[Image from http://www.kurzweilai.net/the-law-of-accelerating-returns] 

Many years ago a highschool student wrote to me asking for an estimate of the processing speed of the human brain. This is a difficult question to answer for many reasons.

One reason is that it is not easy to say how much information is carried by a single neural firing. Some people might say a single neural firing is equal to a single bit flip in a computer, which would be roughly equivalent to 1/64th or 1/128th of a floating point operation (FLOP). However, neurons are not strictly binary. Although it is true they either fire or don't fire, their firing represents the effect of much prior information and the summation of a variety of biochemical and computational factors. I think it is probably impossible to compute with any accuracy how much information is transmitted by a single neuron firing, since it would depend on a huge number of factors such as where the neuron is (in many senses: which species? Which part of the brain? Which individual?), what sort of neurotransmitters are implicated in the firing, how many neurons connect to that neurons, what kind and number of receptors that neuron has etc. However, I am willing to argue (guess) that these effects would almost certainly cancel out the fact that a FLOP involves 64 or 128 (or possibly more) bits, and therefore say it is probably OK, as rough measure, to say that a single neural firing is equivalent to a single FLOP.

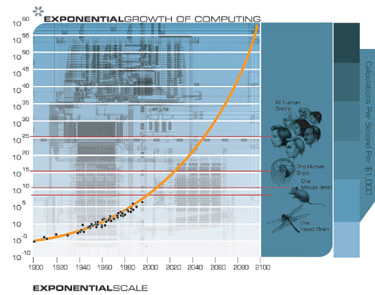
With this 'settled', we can calculate the computing power of the human brain in FLOPs per second (FLOPS) because we have good estimates for the three main variables that enter into it: how many neurons (brain cells) we have, how fast a neuron can fire, and how many cells it connects to. A human being has about 100 billion brain cells. Although different neurons fire at different speeds, as a rough estimate it is reasonable to estimate that a neuron can fire about once every 5 milliseconds, or about 200 times a second. The number of cells each neuron is connected to also varies, but as a rough estimate it is reasonable to say that each neuron connects to 1000 other neurons- so every time a neuron fires, about 1000 other neurons get information about that firing. If we multiply all this out we get 100 billion neurons X 200 firings per second X 1000 connections per firing = 20 million billion calculations per second, which is 20 petaFLOPS.

This estimate might easily be off by at least an order of magnitude- that is, it might be at least 10 times too high or low. It also is a bit misleading because it estimates the raw 'clock speed' of the brain, which is much higher than the number of real useful calculations we do in a second. An apparently much simpler way to approach the problem is to note that the time it takes for the brain to make a really simple decision–like naming a picture or reading a word aloud–is about 300-700 milliseconds. So then we can say that brain can only make about two conscious calculations per second.

However, this is also misleading, for a bunch of reasons. One reason is that well-trained brains can make incredibly complex decisions that quickly. Moreover, even apparently simple tasks like reading a word aloud are actually extremely complex, actually requiring huge amounts of low-level computation. Finally, note that your brain is doing all sorts of things unconsciously at the same time (e.g. maintaining your body and its relation to the world) whenever you are engaged in conscious calculations. So depending on whether you want the raw clock speed, or some higher-level measure of information processing, the question has two answers that differ widely.

This estimate is the same as the estimate by the entrepreneur/futurist Ray Kurzweil (2 x 10^16 computations per second= 20 petaFLOPS). Kurzweil also predicts that we will achieve 20 petaFLOPS on a $1000 desktop PC by 2023. A top end desktop Mac Pro (admittedly, much more than $1000 today, alas) runs at 91 gigaFLOPS. To get to 20 petaFLOPS from 91 gigaFLOPS requires about 17.74 doublings. Computer speed doubles about every 18 months. 17.74 doublings x 1.5 years = 26.6 years. Kurzweil may be a little optimistic, but these calculations suggest that we should see human brain speeds in a desktop computer by 2041. 

But doubling time is also decreasing, so Kurzweil may yet be right.